
We can define these using the Kestrel and Kite respectively, and building from this we will implement the boolean logic that we are all familiar with. These will have to be functions as we don’t have anything else. The combinators which we have just talked about will help us with this.
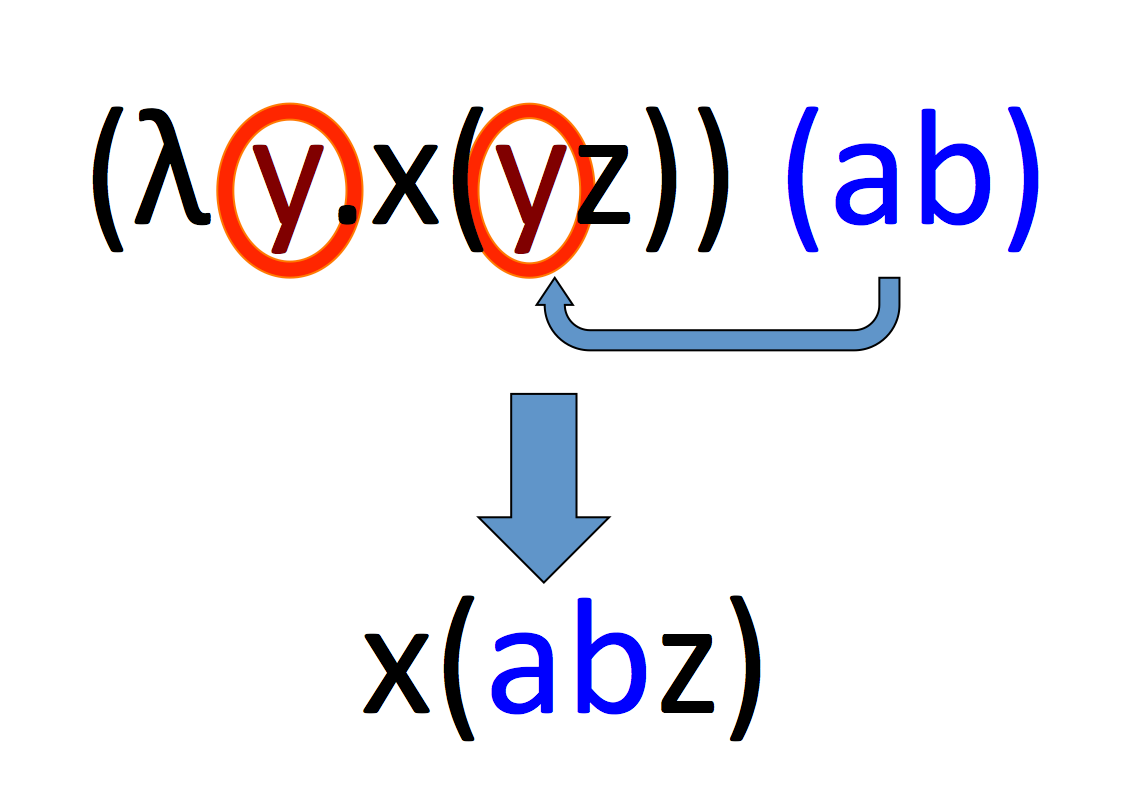
Here I will demonstrate how we can use Church encoding to implement boolean logic. This combinator may seem particularly odd at first sight, but it will come in handy, trust me! Booleans and boolean logic The Mockingbird combinator takes a function and applies it to itself. We can use the Cardinal to flip the arguments of a function as follows: const subtract = a => b => a - b In JavaScript: const C = f => a => b => f(b)(a)

The Cardinal is a function which takes another function, who has 2 arguments, and flips those arguments. The Kite is a function which takes two arguments and returns the second argument. a function which will always return the same value no matter what argument you give it. We can partially apply this function to give us a constant function, ie. The Kestrel is a function which takes two arguments and returns the first argument. The Identity combinator is the simplest combinator of all, it is a function which takes a single argument and returns that argument. You will notice that most of the popular combinators happen to be named after birds, and this is no coincidence! These names originate from a popular puzzle book, To Mock a Mockingbird, whose author Raymond Smullyan decided to give the combinators bird names, in honour of the mathematician and combinatory logician Haskell Curry`s love of birds and bird watching. Some of them may seem trivial and pointless to begin with, but we will see how they can be used to implement formal systems and perform useful computations later on. There are certain combinators which crop up again and again and have useful applications, and we will introduce some of these next. z does not appear in the function parameters so this is not a combinator. CombinatorsĬombinators are simply (pure) functions where all variables in the body of the function are bound to a variable in the head.Ī simple example of this in Lambda calculus:Īnd in JavaScript: const combinator = (x, y) => x Shortly we will look at how we can implement Church encoding for boolean logic and arithmetic of natural numbers. The way we do this is through Church encoding (named after Alonzo Church). In fact, we can compute anything - lambda calculus is Turing complete! Essentially we have a language where the only primitive data type is a function!Īmazingly, from this we can implement operators, data structures and formal systems such as boolean logic and arithmetic. With lambda calculus, all we get out of the box are variables, function abstraction, and function application. This StackBlitz demo contains examples of all of the functions discussed and used in this article.

Much of what I write about in this article is inspired by the puzzle book To Mock a Mockingbird, by Raymond Smullyan, and also the 2 part YouTube series, A Flock of Functions by Gabrial Lebec.

This is a follow up to my previous article, An introduction to Lambda Calculus, explained through JavaScript, which I recommend reading first if you are not familiar with lambda calculus. In particular I will use JavaScript to demonstrate how we can use lambda calculus to implement boolean logic and basic arithmetic. For example, the outermost parentheses are usually not written.In this article I will talk about Church encoding, the mechanism by which we can encode operators and data using lambda calculus. However, some parentheses can be omitted according to certain rules. Thus a lambda term is valid if and only if it can be obtained by repeated application of these three rules. x is a lambda term (called an application).In the simplest form of lambda calculus, terms are built using only the following rules: Lambda calculus consists of constructing lambda terms and performing reduction operations on them. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. It is a universal model of computation that can be used to simulate any Turing machine. Lambda calculus (also written as λ-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. Mathematical-logic system based on functions


 0 kommentar(er)
0 kommentar(er)
